METHOD

DATA

PREPROCESSING

ANALYSIS

Data

The two datasets using in this study is collected by website API. One is from iextrading.com, and one is from financialmodelingprep.com.

Since we want to study sectors, we used sectors name as input file to generate the first dataset. This dataset consists of 20 attributes of 5000 stocks, which mainly focuses on each stock’s information such as date, latest price, volume and etc.

The second dataset is generated by using the stock symbol list we got from the first dataset as query. The second dataset consists of 14 attributes of 5000 stocks. This dataset mainly contains stock’s market information such as beta coefficient, market capitalization and etc.

Finally, we merged these two datasets by the common variable ‘symbol’ and got 14 attributes and about 3000 records.

fig.2-1

Preprocessing

Data Issue

Valid results are usually based on reliable datasets. To make the datasets more reliable, first we identified data issues such as:

missing values
noise data
invalid data
outliers
inconsistent data

fig.2-2

Exploratory data analysis

Correlation

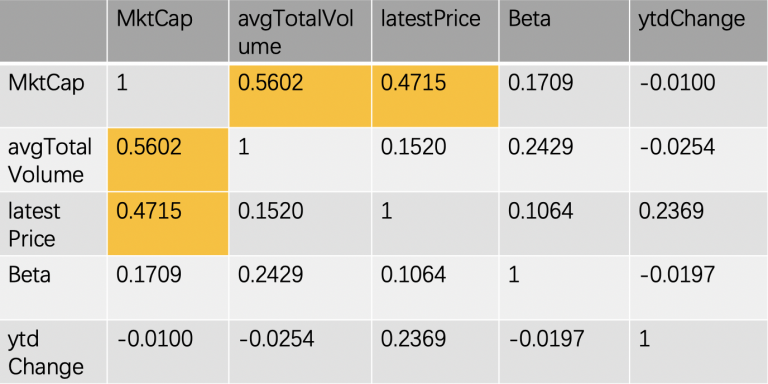
One important part for each study is to exclude the correlated variables, because introducing correlated variables will influence the accuracy of the results. We calculated correlation between each variable for the five numerical variables: beta, market capitalization, latest price, average total volume, year-to-date change. The below table shows the results. We found that MktCap(market capitalization) and avgTotalVolume(average total volume) has a high correlation, as well as MktCap(market capitalization) and latestPrice(latest price). To see the features of these three variables and make decision to remove which variable(s), we plot histogram and did hypothesis testing in the next step.

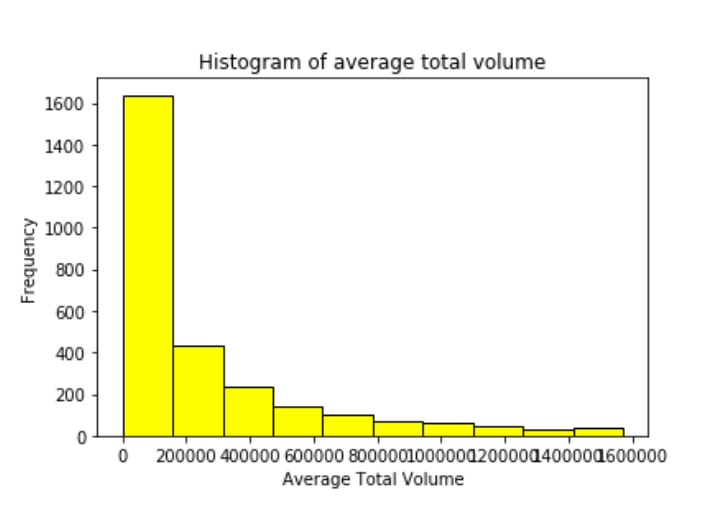
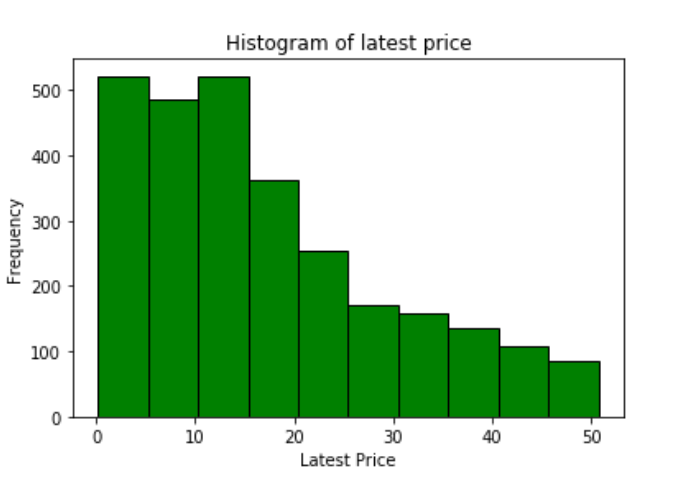
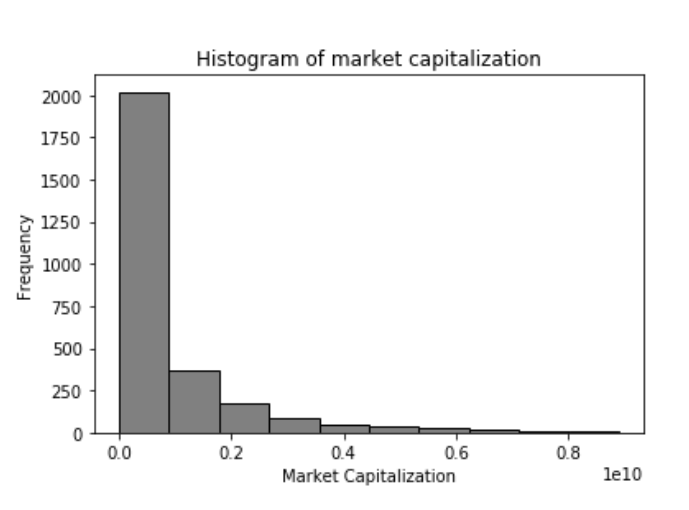
Histograms

From the last histogram, we can see that nearly 70% of stocks’ market capitalization is within 10^9. Therefore, the difference in market capitalization between sectors is not obvious and valuable to investigate. Conclude from both correlation and histogram, we decided to remove market capitalization.

Hypothesis Testing

Applying ANOVA test to latest price and average total volume, we found that the p-value for latest price is near 1. We failed to reject null hypothesis that on average the latest price for 11 sectors are same at any significant level. While, the p-value for average total volume is near 0, therefore, we rejected the null hypothesis and concluded that the average total volume on average is significantly different among sectors. Therefore, we removed latest price. As a result, we used beta, average total volume and year-to-date change as our input variables.

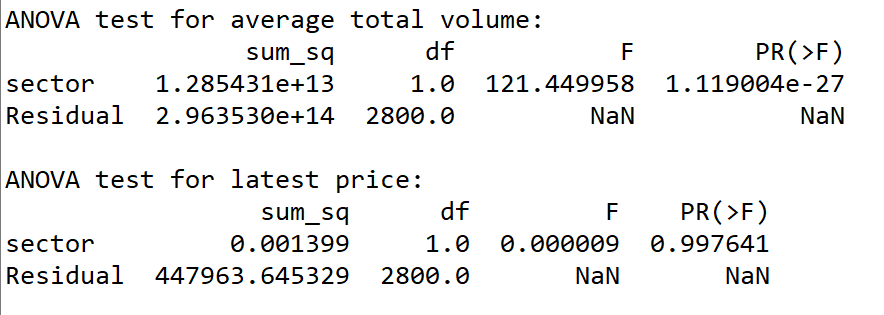
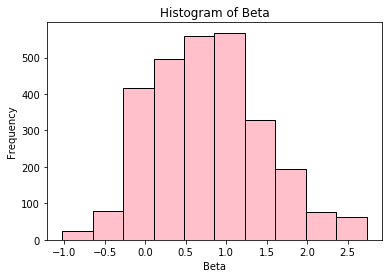
Bins -- for Beta

In this process, we binned three numerical variables and created three new categorical variables accordingly.

First, since Beta is a coefficient to represent risk level of a stock, we binned it and created ‘risk_level’ to store the risk level of stocks. We found that when beta=1, the risk level of a stock can be considered as same as the average risk level of the whole market, so we assign ‘normal’ to represent it; when 0<beta<1, the risk level of a stock can be considered less than the average risk level of the whole market, so we assign ‘small’ to represent it; when beta>1, the risk level of a stock can be considered greater than the average risk level of the whole market, so we assign ‘big’ to represent it; when beta<0, the risk level of a stock can be considered in the opposite direction of the average risk level of the whole market. That is, when the whole stock market becomes riskier, this specific stock with beta<0 is safer, so we assign ‘negative’ to represent it. We created bins according to these criterions and then binned Beta.

Bins -- for average total volume

Average Total Volume can be considered as an indicator, since high average total volume reflects high level of interest in a stock at its current price. We created a new variable called Volume_level. We binned it into 5 categories: A, B, C, D, F, representing the interest level from highest to lowest. We use min-1, 25% quantile, 50% quantile, mean, 75% quantile, max+1 as the bins for this variable. After binning, we can know that stocks with volume level A gaining more interest in the market.

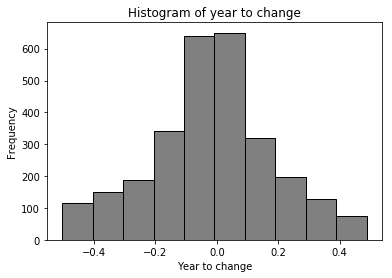
Bins -- for year-to-date change

year-to-date change represents the percentage change of a stock price from the beginning of current year to the current date. Therefore, creating a variable called Change_level to represent the change level is reasonable. We binned it into 5 categories: ++, +, |, -, –, representing the change level from highest to lowest. We use min, 25% quantile, 50% quantile, mean, 75% quantile, max as the bins for this variable. After binning, we can know that price of stocks with change level | do not change much during this time period and price of stocks with change level ++ increases dramatically during this time period.

Analysis

Clustering Analysis

Clustering analysis is used to derive groups such that all the objects in one group share some similarities and objects in different groups are different. The goal of our study is to find the optimal number of clusters of 11 sectors.

fig.2-3

Before starting clustering analysis, we first need to normalize our dataset. We used Min-Max Normalization.

The formula is shown below:

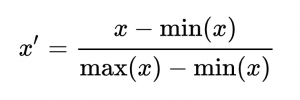
After normalization, all numerical numbers are within the interval [0,1].

fig.2-4

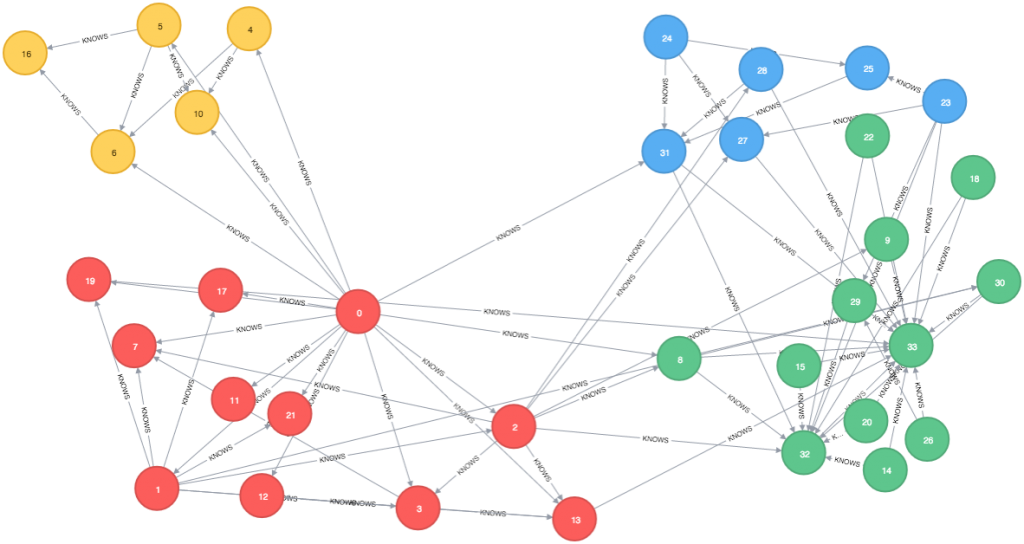
fig.2-5

To derive similarities and differences of stock performance among different sectors, we mainly employed cluster analysis using beta, year-to-date change and average total volume. We employed k-means and hierarchical clustering: we first tried different number of clusters, and then let k=5 since it is a reasonable number of clusters(the optimal number of clustering is 2, but it is a small number for groups. We noticed that the quality decreased with k increasing, so we chose 5 which is not too small and near the optimal number) ; then we used hierarchical clustering as supplement to check the result of k-means clustering since it does not need to pre-specify the number of clusters. In the next step, we investigated which cluster that each sector belongs to. Since there are some sectors belong to more than one clusters, we calculated the percentage of each sectors in each cluster and made the sector belong to the cluster that has its biggest percentage.

Next, we developed a clustering by manually separating these data points into different risk level, change level and volume level. For example, we first counted the number of stocks of each sector in each risk level and made the one dominating this sector as the level of risk for this sector, so that each sector has a risk label: big, small or negative. We repeated this process for change level and volume level and then classified the 11 sectors into 5 new labels which created by merging previous classification.

fig.2-6

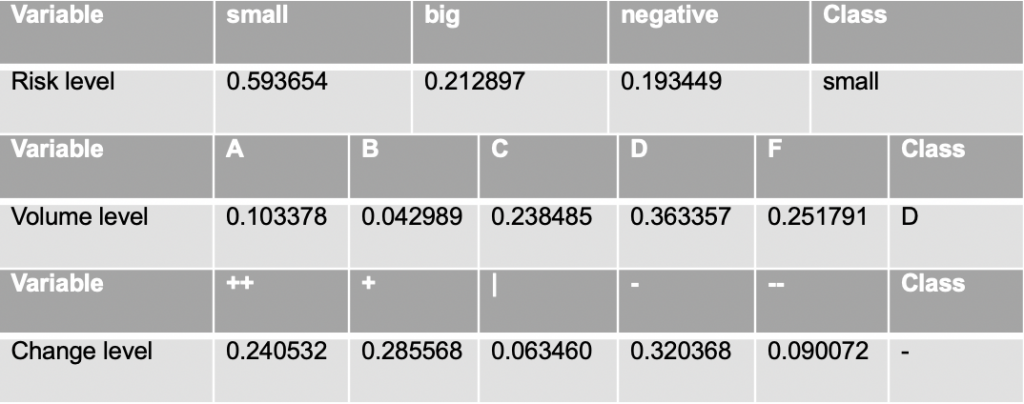
For example, for financial services sector, about 59% stocks have small risk, about 36% stocks have D volume level and about 32% stocks have – change level. Therefore, the label for this sector is small risk, D level volume and – level change.